# 二维数组简介
二维数组是一种结构较为特殊的数组,只是将数组中的每个元素变成了一维数组。
所以二维数组的本质上仍然是一个一维数组,内部的一维数组仍然从索引 0 开始,我们可以将它看作一个矩阵,并处理矩阵的相关问题。
# 示例
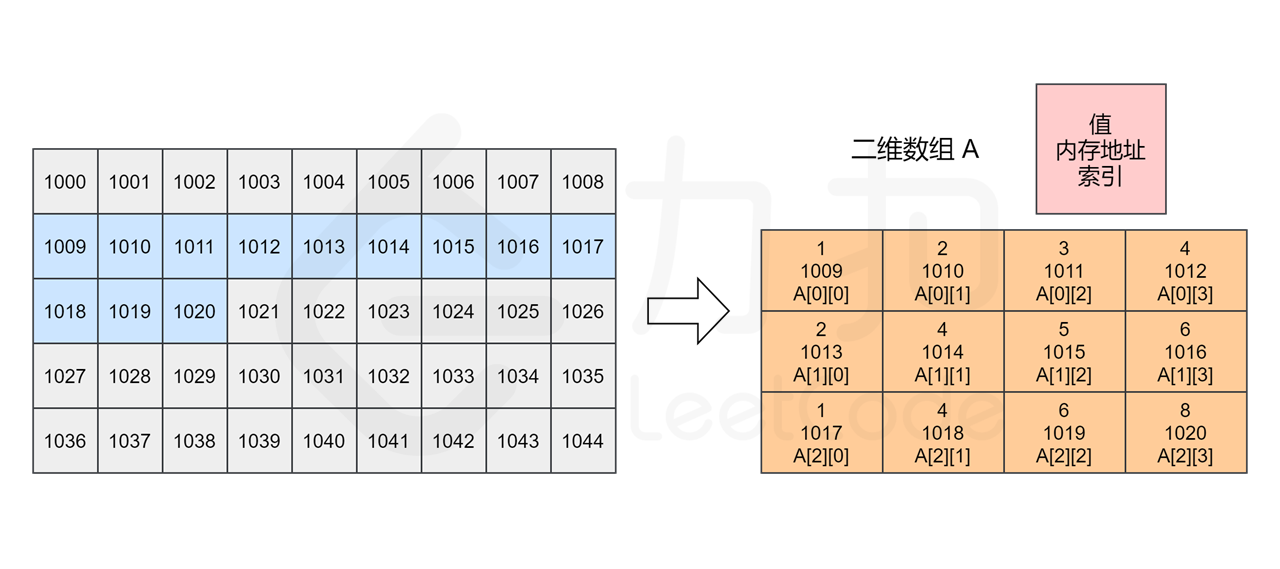
类似一维数组,对于一个二维数组 A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]],计算机同样会在内存中申请一段 连续 的空间,并记录第一行数组的索引位置,即 A[0][0] 的内存地址,它的索引与内存地址的关系如下图所示。
# 旋转矩阵
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
];
原地旋转输入矩阵,使其变为:
[
[7, 4, 1],
[8, 5, 2],
[9, 6, 3]
];
示例 2:
给定
matrix = [
[5, 1, 9, 11],
[2, 4, 8, 10],
[13, 3, 6, 7],
[15, 14, 12, 16]
];
原地旋转输入矩阵,使其变为:
[
[15, 13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7, 10, 11]
];
// 方法一
// 对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
var rotate = function(matrix) {
var newMatrix = [];
var n = matrix.length;
for (var i = 0; i < matrix.length; i++) {
for (var j = 0; j < matrix[i].length; j++) {
if (!newMatrix[j]) {
newMatrix[j] = [];
}
newMatrix[j][n - i - 1] = matrix[i][j];
}
}
for (var i = 0; i < matrix.length; i++) {
for (var j = 0; j < matrix[i].length; j++) {
matrix[i][j] = newMatrix[i][j];
}
}
};
# 方法二:原地旋转交换
根据方法一可推出,旋转时,下面四项处于一个循环中,并且每一项旋转后的位置就是下一项所在的位置!
matrix[row][col]
matrix[col][n−row−1]
matrix[n−row−1][n−col−1]
matrix[n−col−1][row]
因此我们可以使用一个临时变量 temp 完成这四项的原地交换
temp = matrix[row][col]
matrix[row][col] = matrix[n−col−1][row]
matrix[n−col−1][row] = matrix[n−row−1][n−col−1]
matrix[n−row−1][n−col−1] = matrix[col][n−row−1]
matrix[col][n−row−1] = temp
var rotate = function(matrix) {
var n = matrix.length;
for (var i = 0; i < Math.floor(n / 2); i++) {
for (var j = 0; j < n / 2; j++) {
var temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
};
# 方法三:用翻转代替旋转
先水平翻转,再主对角线翻转
5 1 9 11 15 14 12 16
2 4 8 10 13 3 6 7
------------ =水平翻转=> ------------
13 3 6 7 2 4 8 10
15 14 12 16 5 1 9 11
15 14 12 16 15 13 2 5
13 3 6 7 =主对角线翻转=> 14 3 4 1
2 4 8 10 12 6 8 9
5 1 9 11 16 7 10 11
水平轴翻转:
matrix[i][j] -> matrix[n−i−1][j]
主对角线翻转:
matrix[i][j] -> matrix[j][i]
上面两个式子联立可得:
matrix[i][j] -> matrix[j][n-i-1]
这于方法一和方法二中的关键等式是一致的:newMatrix[j][n−i−1]=matrix[i][j]
所以先水平翻转,再主对角线翻转方法是可行的
var rotate = function(matrix) {
var n = matrix.length;
// 水平翻转
for (var i = 0; i < Math.floor(n / 2); i++) {
for (var j = 0; j < n; j++) {
var temp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = temp;
}
}
// 主对角线翻转
for (var i = 0; i < n; i++) {
for (var j = i + 1; j < n; j++) {
var temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
};
# 零矩阵
编写一种算法,若 M × N 矩阵中某个元素为 0,则将其所在的行与列清零。 示例 1:
输入:
[
[1, 1, 1],
[1, 0, 1],
[1, 1, 1]
];
输出:
[
[1, 0, 1],
[0, 0, 0],
[1, 0, 1]
];
示例 2:
输入:
[
[0, 1, 2, 0],
[3, 4, 5, 2],
[1, 3, 1, 5]
];
输出:
[
[0, 0, 0, 0],
[0, 4, 5, 0],
[0, 3, 1, 0]
];
var setZeroes = function(matrix) {
var zeroRow = new Set();
var zeroCol = new Set();
for (var i = 0; i < matrix.length; i++) {
for (var j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] === 0) {
zeroRow.add(i);
zeroCol.add(j);
}
}
}
// 行清零
for (var i of zeroRow) {
for (var j = 0; j < matrix[i].length; j++) {
matrix[i][j] = 0;
}
}
// 列清零
for (var j of zeroCol) {
for (var i = 0; i < matrix.length; i++) {
matrix[i][j] = 0;
}
}
};
作者:力扣 (LeetCode)
链接:https://leetcode-cn.com/leetbook/read/array-and-string/chg0d/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。