# 双指针技巧

# 链表中的双指针

在数组和字符串中，主要有 2 种双指针的使用场景：

两个指针从不同位置出发：一个从始端开始，另一个从末端开始；
两个指针以不同速度移动：一个指针快一些，另一个指针慢一些。

对于单链表，因为我们只能在一个方向上遍历链表，所以第一种情景可能无法工作。然而，第二种情景，也被称为慢指针和快指针技巧，是非常有用的。

# 判断环形链表

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：
你能用 O(1)（即，常量）内存解决此问题吗？

// 方法一：哈希表
var hasCycle = function(head) {
  if (!head || !head.next || !head.next.next) {
    return false;
  }
  var hashMap = new WeakMap();
  var current = head;
  while (hashMap.get(current) === undefined) {
    if (current.next === null) {
      return false;
    }
    hashMap.set(current, 1);
    current = current.next;
  }
  return true;
};

// 方法二：快慢指针
var hasCycle = function(head) {
  if (!head || !head.next || !head.next.next) {
    return false;
  }
  var slow = head;
  var fast = head.next;
  // 1.如果是循环链表，那么最终快慢指针肯定会相遇
  // 2.while循环是通过判断快慢指针是否相等作为条件，所以让快指针初始为head.next，
  // 这并不会影响判断逻辑，因此只要存在循环，快指针从慢指针之前的任意位置开始最终都会与慢指针相遇
  while (fast !== slow) {
    // 可以在当前循环判断fast.next.next，
    // 也可以不对fast.next.next进行判断，因为会在下一个循环进行判断
    if (!fast || !fast.next) {
      return false;
    }
    slow = slow.next;
    fast = fast.next.next;
  }
  return true;
};

# 判断环形链表 2

在 判断环形链表 的基础上，增加条件：
给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。
看图方便理解：
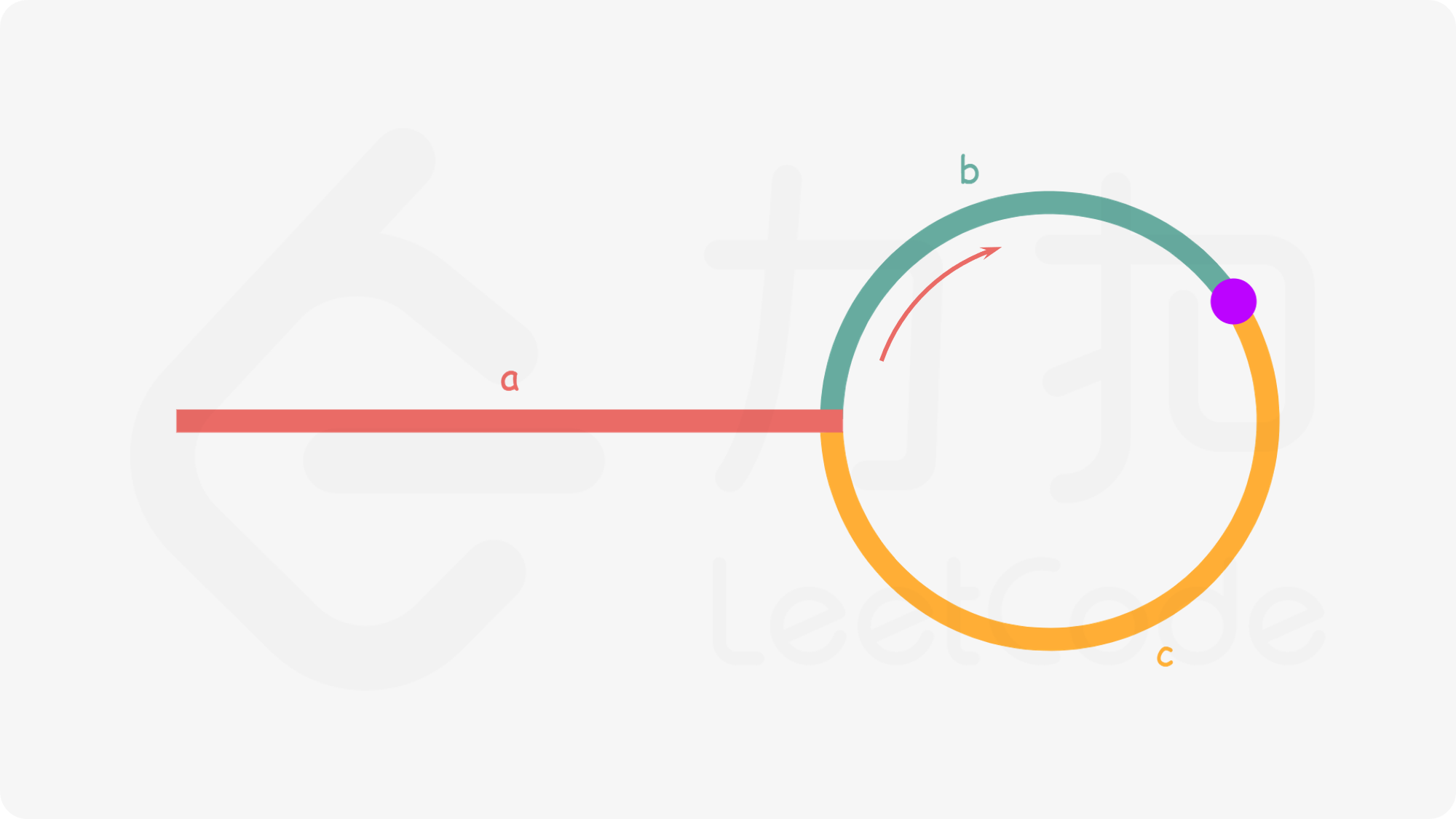
环形链表的快慢指针

// 方法一：哈希表
var detectCycle = function(head) {
  if (!head || !head.next) {
    return null;
  }
  var current = head;
  var map = new WeakMap();
  while (map.get(current) === undefined) {
    if (current.next === null) {
      return null;
    }
    map.set(current, 1);
    current = current.next;
  }
  return current;
};

// 方法二：快慢指针
var detectCycle = function(head) {
  if (!head || !head.next || !head.next.next) {
    return null;
  }
  // 关键点，快慢指针都从起始点出发，当快慢指针相遇时（上图中的紫色点）可得：
  // 慢指针走了：a + b
  // 快指针走了： a + b + c + b
  // 这里为什么可以肯定慢指针在环形内最多只走一圈，2个指针就能相遇呢？
  // 因为，快指针的速度是慢指针的2倍，慢指针如果走完一圈，快指针肯定已经走完2圈了，
  // 所以必定在一圈内2个指针就会相遇
  // 所以： 2(a + b) = a + b + c + b => a = c
  // 也就是说，相遇点移动到入环点的的距离等于起始点移动到入环点的距离
  // 因此相遇时新增第三个指针ptr，从起始点开始每步移动一个距离，慢指针也继续移动一个距离
  // 那么ptr指针和慢指针将在入环点相遇
  var slow = head;
  var fast = head;

  while (fast !== null && fast.next !== null) {
    slow = slow.next;
    if (fast.next !== null) {
      fast = fast.next.next;
    } else {
      return null;
    }
    if (fast === slow) {
      var ptr = head;
      while (ptr !== slow) {
        slow = slow.next;
        ptr = ptr.next;
      }
      return ptr;
    }
  }
  return null;
};

# 相交链表

编写一个程序，找到两个单链表相交的起始节点。
如下面的两个链表：相交链表-示例1 在节点 c1 开始相交。

注意：

如果两个链表没有交点，返回 null.
在返回结果后，两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

方法一: 暴力法
对链表 A 中的每一个结点 a<i> ，遍历整个链表 B 并检查链表 B 中是否存在结点和 a<i> 相同。
复杂度分析
时间复杂度 : (mn)。
空间复杂度 : O(1)。

方法二: 哈希表法
遍历链表 A 并将每个结点的地址/引用存储在哈希表中。然后检查链表 B 中的每一个结点 b<i> 是否在哈希表中。若在，则 b<i> 为相交结点。
复杂度分析
时间复杂度 : (m+n)。
空间复杂度 : O(m)或 O(n)。

方法三：双指针法
创建两个指针 pA 和 pB，分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。
当 pA 到达链表的尾部时，将它重定位到链表 B 的头结点 (你没看错，就是链表 B); 类似的，当 pB 到达链表的尾部时，将它重定位到链表 A 的头结点。
若在某一时刻 pA 和 pB 相遇，则 pA/pB 为相交结点。
想弄清楚为什么这样可行, 可以考虑以下两个链表: A={1,3,5,7,9,11} 和 B={2,4,9,11}，相交于结点 9。由于 B.length (=4) < A.length (=6)，pB 比 pA 少经过 2 个结点，会先到达尾部。将 pB 重定向到 A 的头结点，pA 重定向到 B 的头结点后，pB 要比 pA 多走 2 个结点。因此，它们会同时到达交点。如果两个链表存在相交，它们末尾的结点必然相同。因此当 pA/pB 到达链表结尾时，记录下链表 A/B 对应的元素。若最后元素不相同，则两个链表不相交。
复杂度分析
时间复杂度 : O(m+n)。
空间复杂度 : O(1)。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function(headA, headB) {
  if (!headA || !headB) {
    return null;
  }
  var AStep = headA;
  var BStep = headB;
  var count = 0;
  while (count < 3) {
    if (AStep === null) {
      AStep = headB;
      count++;
    }
    if (BStep === null) {
      BStep = headA;
      count++;
    }
    if (AStep === BStep) {
      return AStep;
    }
    AStep = AStep.next;
    BStep = BStep.next;
  }
  return null;
};

# 删除链表的倒数第 N 个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后，链表变为 1->2->3->5.

方法一：递归到尾节点，然后返回，返回计数到 N，即可得到倒数第 N 个节点

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
var removeNthFromEnd = function(head, n) {
  var target = null;
  var prevNode = null;
  var count = 0;
  function getNext(node) {
    if (node.next) {
      getNext(node.next);
    }
    count++;
    if (count === n) {
      target = node;
    } else if (count === n + 1) {
      prevNode = node;
    }
  }
  getNext(head);
  if (!prevNode) {
    head = target.next;
  } else {
    prevNode.next = target.next;
  }
  return head;
};

方法二：双指针，前一个指针先走 N 次，第二个指针再从头开始走，这样第一个指针到达链表尾部时，第二个指针就正好到达倒数第 N 个

var removeNthFromEnd = function(head, n) {
  if (!head) {
    return null;
  }
  var p1 = head;
  var p2 = head;
  var prev = null;
  // p1先走N次，“根据下标从0开始算”，所以用n-1判断
  while (n - 1) {
    p1 = p1.next;
    n--;
  }
  // p1移动到链表尾部
  while (p1.next) {
    p1 = p1.next;
    prev = p2;
    p2 = p2.next;
  }
  if (!prev) {
    head = p2.next;
  } else {
    prev.next = p2.next;
  }
  return head;
};

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/linked-list/jbex5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

← 单链表金典问题 →